Two Pointers

Often we are working with an array (or a linked list) and we want to find some subset of the array with a particular property. For example, consider the following problem:

Two Sum (Sorted)

We are given an array of numbers and a target number. Write a function that returns the two indices of numbers in the array that sum to the target number. You can assume there is always a unique solution.

Example instance where array = [1,2,5,6,7,10,20] and target = 9

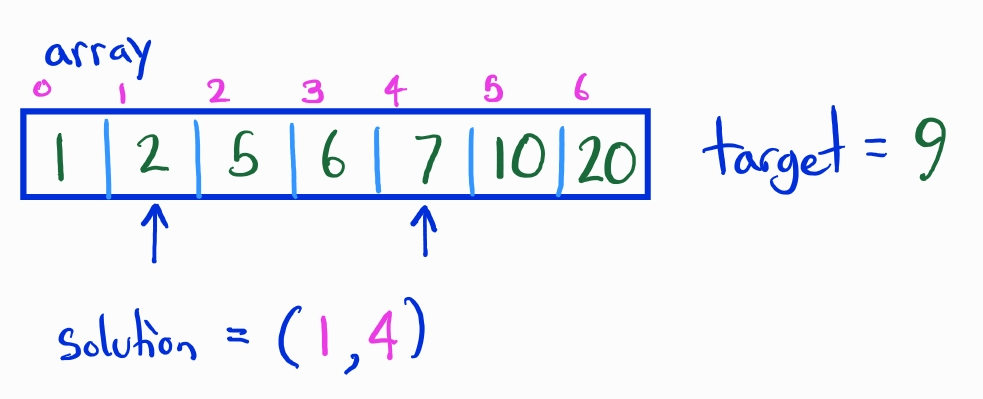
Often we can find the right subset by brute force and checking all possible subsets, but this is inefficient. If we want to check all pairs in the array the runtime is ${n \choose 2} = n(n-1)/2 = O(n^2)$

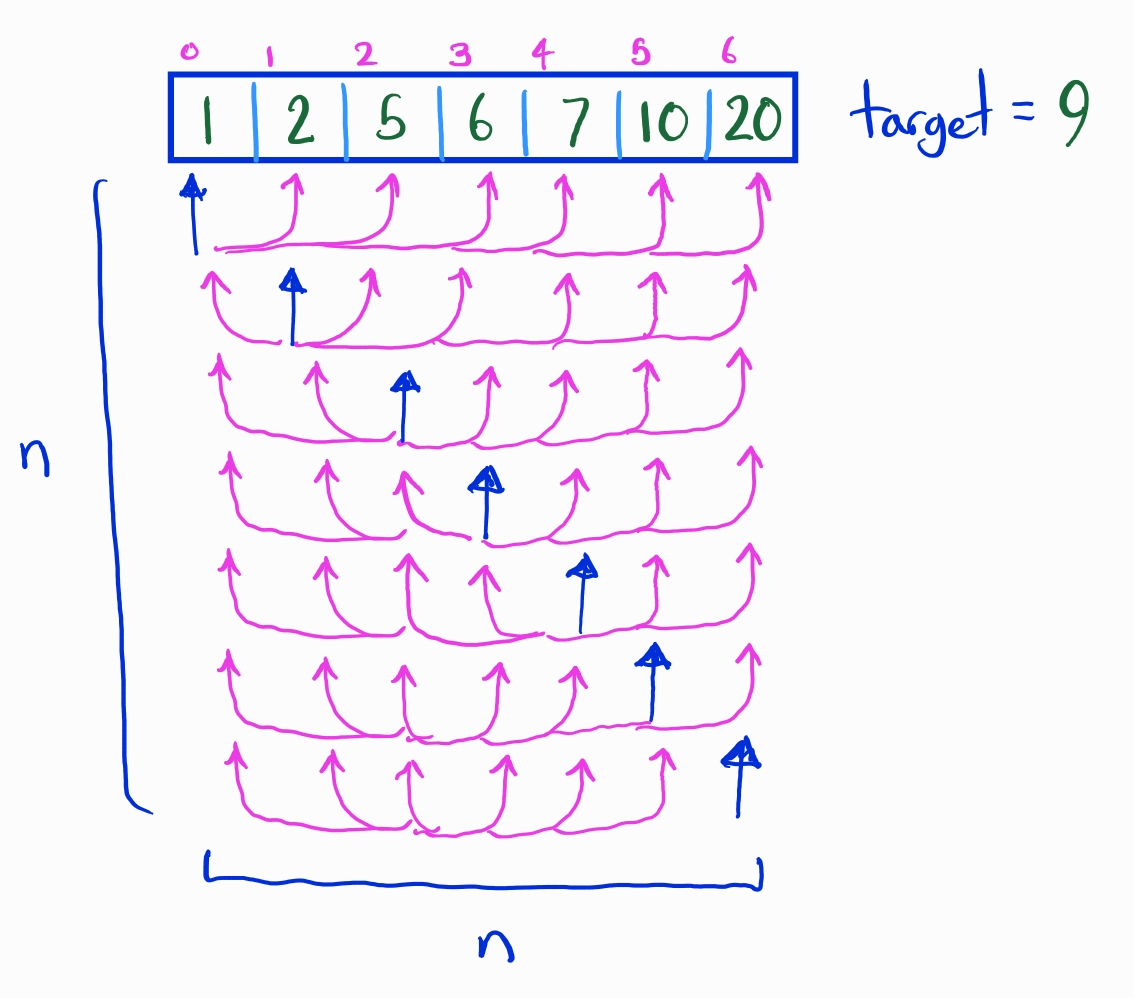
A more efficient way (when the array happens to be sorted) is to search through the array with the "two pointers approach". This is when we run a loop while we keep track of two indices. We update both of these indexes a maximum of $n$ times based on some simple criteria to find the array subset we are looking for.

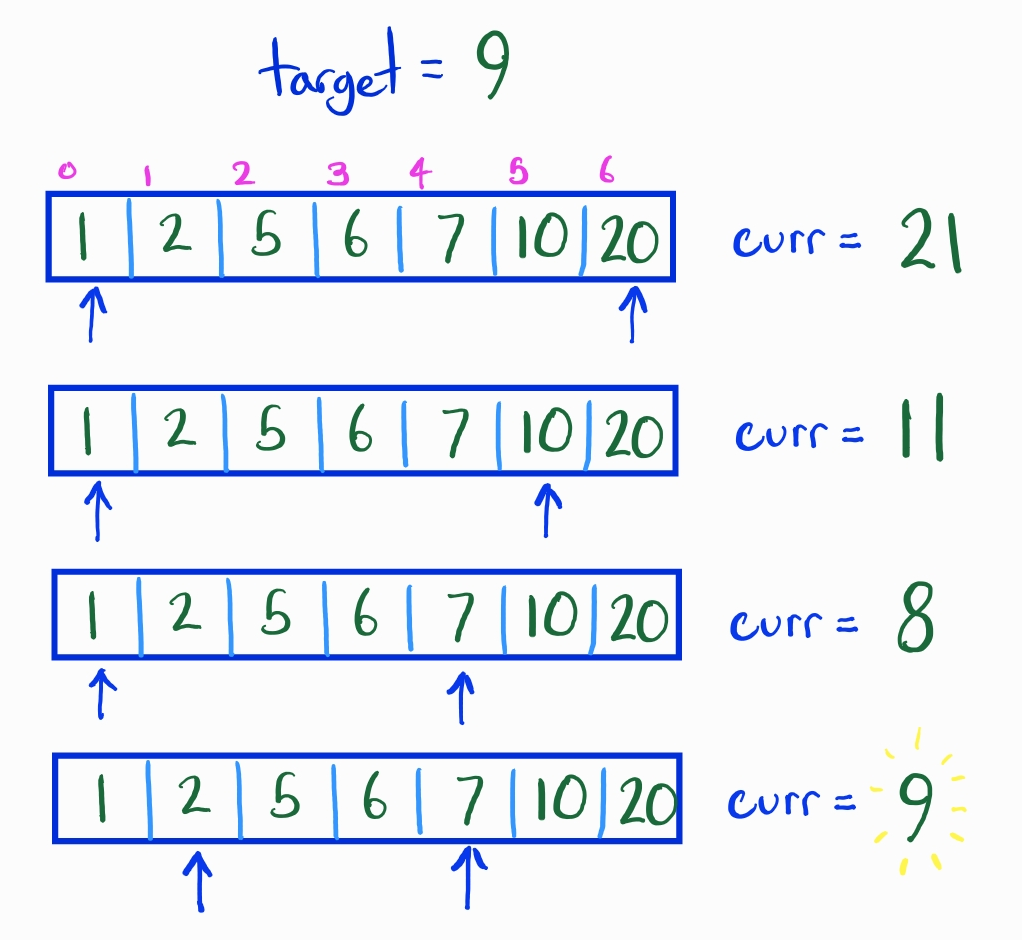
Let’s look at our previous problem again and try the following:

• Start with the "pointers" at either end of the array
  • ptr1 <-- 0, ptr2 <-- n-1
• In a loop → check the current sum of numbers that are "pointed" to
  • if sum > target move the right pointer left by one i.e. ptr2 -= 1
  • if sum < target move the left pointer to the right by one i.e. ptr1 += 1
  • else sum==target and we return the indices as are solution

Skeleton Proof

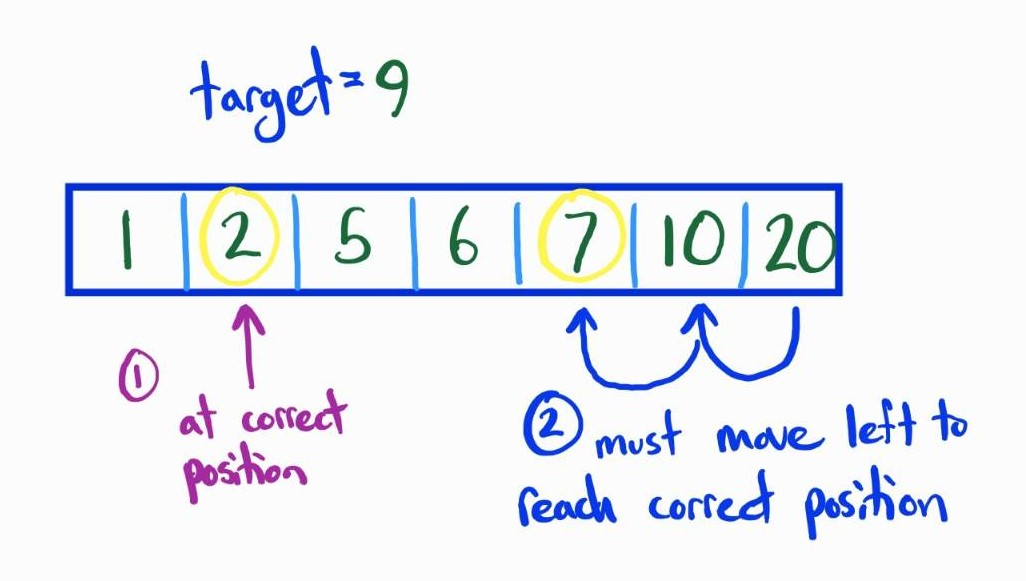
Why does this always work?

Let’s pretend it doesn't: well then either we missed the correct indices by first passing over the correct position for the leftmost pointer (which only moves right) or by passing over the correct position for the rightmost pointer (which only moves left):

Case 1: leftmost pointer missed when moving right…

Then at some point the leftmost pointer was at the correct position and the rightmost pointer was right of its correct position. But at this point the current sum must be greater than the target because the array is sorted, so the rightmost pointer must move left until we reach the other correct index.

Therefore, we actually can not miss and the two-pointer algorithm is correct!

Case 2: rightmost pointer missed when moving left…

same kind of logic as case 1

Problems for this week

(easy) two-sum

"Given an array of integers numsand an integer target, return indices of the two numbers such that they add up to target ." Assume there is exactly one solution and do not use the same array element twice.

Note: In the example given above, we assumed that the array was sorted, but it isn’t necessarily sorted for this question. You can sort this array to begin to simulate trying to code the example!

(easy) remove-duplicates-from-sorted-array

"Given an integer array nums sorted in non-decreasing order, remove the duplicates in-place such that each unique element appears only once. The relative order of the elements should be kept the same."

(easy) squares-of-a-sorted-array

"Given an integer array numssorted in non-decreasing order, return an array of the squares of each number sorted in non-decreasing order." The tricky part is the presence of positive and negative numbers results in an unsorted array after squaring.

(medium) 3sum

"Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0. Notice that the solution set must not contain duplicate triplets."

(medium) 3sum-closest

"Given an integer array nums of length n and an integer target, find three integers in nums such that the sum is closest to target. Return the sum of the three integers. You may assume that each input would have exactly one solution."

(medium) 3sum-smaller

"Given an integer array nums of length n and an integer target, find three integers in nums such that the sum is closest to target. Return the sum of the three integers. You may assume that each input would have exactly one solution."

(medium) subarray-product-less-than-k

"Given an array of integers nums and an integer k, return the number of contiguous subarrays where the product of all the elements in the subarray is strictly less than k."

(medium) sort-colors

"Given an array nums with n objects colored red, white, or blue, sort them in-place so that objects of the same color are adjacent, with the colors in the order red, white, and blue. We will use the integers 0, 1, and 2 to represent the color red, white, and blue, respectively. You must solve this problem without using the library's sort function."

(medium) 4sum

"Given an array nums of n integers, return an array of all the unique quadruplets [nums[a], nums[b], nums[c], nums[d]] such that:

• 0 <= a, b, c, d <= n
• a, b, c, and d are distinct.
• nums[a] + nums[b] + nums[c] + nums[d] == target

You may return the answer in any order."

(easy) (could maybe be medium though) backspace-string-compare

"Given two strings s and t, return true if they are equal when both are typed into empty text editors. '#' means a backspace character. Note that after backspacing an empty text, the text will continue empty."

(medium) shortest-unsorted-continuous-subarray

"Given an integer array nums, you need to find one continuous subarray that if you only sort this subarray in ascending order, then the whole array will be sorted in ascending order. Return the shortest such subarray and output its length."

(hard) trapping-rain-water

"Given nnon-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining."