2D Array Traversal

Sometimes we need a way to store data in a matrix format. One such way of doing this is by storing values in a 2D array. This is when we have arrays as the elements of another array

e.g. my_array = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] is the matrix $\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$

Now consider the following problem:

Number of Negative Numbers in a sorted 2D array

Given a 2D array of integers that is sorted in non-increasing order (from largest to smallest) in both the columns and the rows, write a function the counts the number of negative entries.

Example instance where the answer is 5 negative entries: my_array = [[5, 4, 3], [2,-1,-4], [-2,-2,-5]]

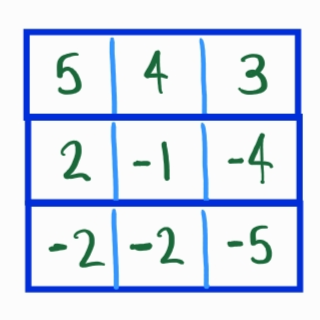
The naive brute force approach to solve this problem is to iterate through every entry increasing your count when you come across a negative integer:

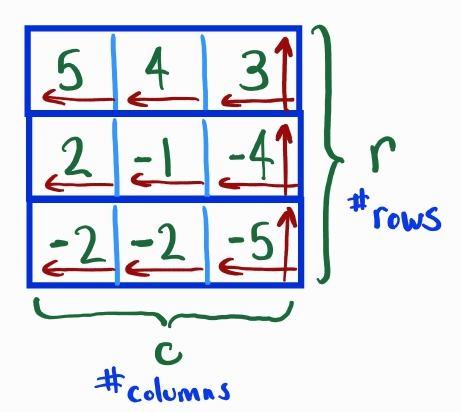
The runtime complexity for this approach is $\Theta(r \times c)$ and the memory complexity is $\Theta(1)$

We can speed up our solution by iterating backwards through the rows and columns and stopping early (breaking out of a loop) when/if we see a positive number.

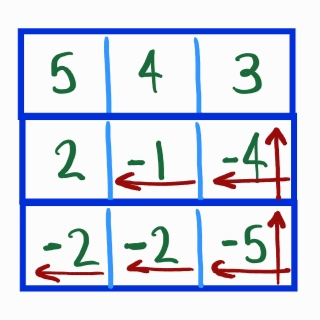
The runtime complexity for this approach is $\Theta(k)$ where $k$ is the number of negative entries. The memory complexity is still $\Theta(1)$.

Problems for this Week

(easy) count-negative-numbers-in-a-sorted-matrix

Given a m x n matrix grid which is sorted in non-increasing order both row-wise and column-wise, return the number of negative numbers ingrid

(easy) transpose-matrix

Given a 2D integer array matrix, return the transpose of matrix. The transpose of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.

(easy) → bruteforce, (medium) → efficient. set-matrix-zeroes

Given an m x n integer matrix matrix, if an element is 0, set its entire row and column to 0's. You must do it in place.

(medium) number-of-islands

Given an m x n 2D binary grid grid which represents a map of '1's (land) and '0's (water), return the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

(medium) max-area-of-island

You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water. The area of an island is the number of cells with a value 1 in the island. Return the maximum area of an island in grid. If there is no island, return 0.

(medium) number-of-closed-islands

Given a 2D grid consisting of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.Return the number of closed islands.

(medium) diagonal-traverse-ii

Given a 2D integer array nums, return all elements of nums in diagonal order as shown in the below images.